问题
解答题
判断下列函数是否存在零点,如果存在,请求出.
(1)f(x)=-8x2+7x+1;
(2)f(x)=x2+x+2;
(3)f(x)=x3+1。
答案
解:(1)∵f(x)=-8x2+7x+1=-(8x+1)(x-1),
令f(x)=0可解得x=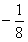 或x=1,
或x=1,
所以函数的零点为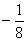 和1.
和1.
(2)令x2+x+2=0,因为△=12-4×1×2=-7<0,
所以方程无实数解,
所以f(x)=x2+x+2不存在零点.
(3)因为f(x)=x3+1=(x+1)(x2-x+1),
令(x+1)(x2-x+1)=0,
解得x=-1,所以函数的零点为-1.
