解：若a=0，则函数f（x）=2x-3在区间 [-1，1]上没有零点，

下面就a≠0时分三种情况讨论：

 （1）方程f（x）=0在区间[ -1，1]上有重根

此时Δ=4（2a²+6a+1）=0

解得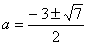

当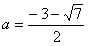时，f（x）=0的重根x=；

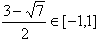当时，f（x）=0的重根；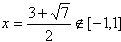

故当方程f（x）=0在区间[ -1，1]上有重根时，；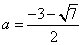

（2）f（x）在区间[ -1，1]上只有一个零点且不是f（x）=0的重根

此时有f（-1）f（1）≤0

∵f（-1）=a-5

f（1）=a-1

∴（a-5）（a-1）≤0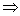1≤a≤5

∵当a=5时，方程f（x）=0在区间[ -1，1]上有两个相异实根，

故当方程f（x）=0在区间[-1，1]上只有一个根且不是重根时，1≤a<5。

（3）方程f（x）=0在区间[ -1，1]上有两相异实根

因为函数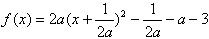

其图象的对称轴方程为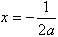

a应满足：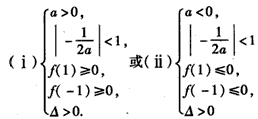

解不等式组（i）得a≥5

解不等式组（ii）得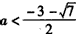

故当方程f（x）=0在区间[ -1，1]上有两个相异实根时

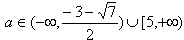
注意到当1≤a<5时，f（-1）f（1）≤0，方程f（x）=0在区间 [ -1，1]上有根；

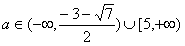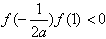当时，由于，且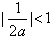

方程f（x）=0在[ -1，1]上有根；

当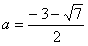时，方程f（x）=0在区间[-1，1]有根

综上所述，函数y=f（x）在区间[ -1，1]上有零点，则a的取值范围是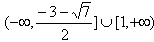。