问题
解答题
一个口袋中装有大小相同的2个白球和3个黑球。
（Ⅰ）从中摸出两个球，求两球恰好颜色不同的概率；
（Ⅱ）从中摸出一个球，放回后再摸出一个球，求两球恰好颜色不同的概率。
答案
解：（Ⅰ）记“摸出两个球，两球恰好颜色不同”为A，摸出两球共有方法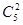
=10种，
1分
其中，两球一白一黑有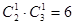
种。 2分
∴
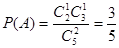。 4分
（Ⅱ）解法一：记摸出一球，放回后再摸出一个球“两球恰好颜色不同”为B，摸出一球得白球的概率为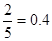
， 5分
摸出一球得黑球的概率为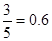
， 6分
∴
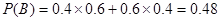。 8分
解法二：“有放回摸两次，颜色不同”指“先白再黑”或“先黑再白”。
∴
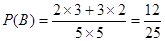。 6分
∴“有放回摸两次，颜色不同”的概率为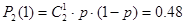
。 8分
本题考查等可能事件的概率公式，本题解题的关键是写出试验发生包含的事件数和满足条件的事件数，再用公式求解
（Ⅰ）本题是一个等可能事件的概率，摸出两个球共有方法C52种，其中两球一白一黑有6种，得到概率．
（II）摸出一球得白球的概率为2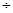
5
=0.4，摸出一球得黑球的概率为3 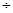5=0.6，“放回后再摸一次，两球颜色不同”指“先白再黑”或“先黑再白”，这两种情况是互斥的，得到概率