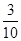
分析：把白球编号为1，2，黑球记为a，b，c，用列举法求得共有10种摸法．由于其中摸出两个黑球的方法有3种，由此可得摸出2个黑球的概率．

解答：解：白球编号为1，2，黑球记为a，b，c，

共有10种摸法：（1，2），（1，a），（1，b），（1，c），（2，a），（2，b），（2，c），

（a，b），（a，c），（b，c）．--（4分）

其中，摸出两个黑球的方法有 （a，b），（a，c），（b，c）3种，

故摸出2个黑球的概率为 p=．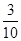

点评：本题考查古典概型问题，可以列举出试验发生包含的事件和满足条件的事件，应用列举法来解题是这一部分的最主

要思想，属于基础题．