问题
选择题
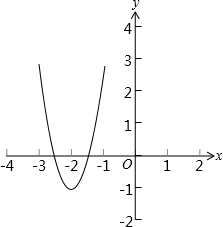
已知抛物线y=ax2+bx+c中,4a-b=0,a-b+c>0,抛物线与x轴有两个不同的交点,且这两个交点之间的距离小于2,则下列判断错误的是( )
A.abc<0
B.c>0
C.4a>c
D.a+b+c>0
答案
∵4a-b=0,∴抛物线的对称轴为x=-
=-2b 2a
∵a-b+c>0,
∴当x=-1时,y>0,
∵抛物线与x轴有两个不同的交点且这两个交点之间的距离小于2,
∴抛物线与x轴的两个交点的横坐标位于-3与-1之间,b2-4ac>0
∴16a2-4ac=4a(4a-c)>0
据条件得图象:
∴a>0,b>0,c>0,
∴abc>0,4a-c>0,
∴4a>c
当x=1时,y=a+b+c>0
故选A.