问题
选择题
已知函数f(x)=
①d<a;②d>b;③d<c;④d>c.其中可能成立的个数为( )
|
答案
解:因为函数f(x)= ?lnx在(0,+∞)上是减函数,
?lnx在(0,+∞)上是减函数,
又因为f(c)<0<f(a)<f(b),
所以a<b<c,又因为零点就是两函数图象的交点,
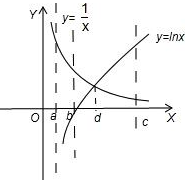
在同一坐标系内画出函数y= 与y=lnx的图象,
与y=lnx的图象,
如图a、b、c,d的位置如图所示只有②③成立.
故可能成立的有两个.
故选B.
已知函数f(x)=
①d<a;②d>b;③d<c;④d>c.其中可能成立的个数为( )
|
解:因为函数f(x)= ?lnx在(0,+∞)上是减函数,
?lnx在(0,+∞)上是减函数,
又因为f(c)<0<f(a)<f(b),
所以a<b<c,又因为零点就是两函数图象的交点,
在同一坐标系内画出函数y= 与y=lnx的图象,
与y=lnx的图象,
如图a、b、c,d的位置如图所示只有②③成立.
故可能成立的有两个.
故选B.
