问题
解答题
若函数f(x)=x2+ax+2b在区间(0,1)、(1,2)内各有一个零点,求
|
答案
由已知得:
⇒(4分)f(0)>0 f(1)<0 f(2)>0
⇒2b>0 a+2b+1<0 2a+2b+4>0
(6分)b>0 a+2b+1<0 a+b+2>0
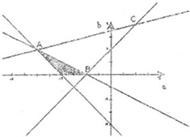
其表示得区域M如图:((9分)
表示C(1,2)与M区域中的点(a,b)连线的斜率.b-2 a-1
A(-3,1),B(-1,0)kCA=
,kCB=11 4
从图中可知
∈(b-2 a-1
,1)1 4
