问题
填空题
若f（x）=ax+b-1（0＜a≤1）在[0，1]上有零点，则b-2a的最小值为______．
答案
由已知得：
或f(0)≥0 f(1)≤0
（4分）f(0)≤0 f(1)≥0
∴
或b-1≥0 a+b-1≤0 b-1≤0 a+b-1≥0
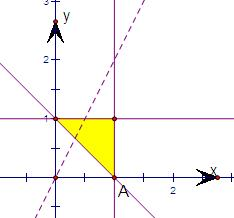
其表示得区域M如图：（（9分）
当直线z=b-2a过点A（1，0）时，b-2a取最小值，最小值为-2．
故答案为：-2．
搜题请搜索小程序“爱下问搜题”