如图，质量m=2kg的物体静止于水平地面的A处，A、B间距L=20m。用大小为30N，沿水平方向的外力拉此物体，经t0=2s拉至B处。(sin37º=0.6，cos37º=0.8，g取10m/s2)
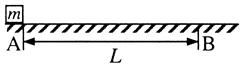
(1)求物体与地面间的动摩擦因数μ；
(2)用大小为30N，与水平方向成37°的力斜向上拉此物体，使物体从A处由静止开始运动并能到达B处，求该力作用的最短时间t。（答案可带根号）
(1)0.5(2)
s
题目分析：(1)物体做匀加速运动 
(1分)
由牛顿第二定律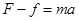 
（1分）
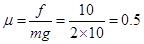（1分）
∴
(1分)
(2)设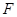
作用的最短时间为
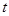，小车先以大小为
的加速度匀加速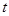秒，撤去外力后，以大小为
，的加速度匀减速
秒到达B处，速度恰为0，由牛顿定律
(1分)
∴
(1分)
（1分）
由于匀加速阶段的末速度即为匀减速阶段的初速度，因此有
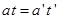（1分）
∴
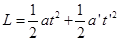（1分）
∴
s（1分）
（2）另解：设力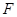作用的最短时间为t，相应的位移为s，物体到达B处速度恰为0，由动能定理
（3分）
由牛顿定律
（1分）
∵
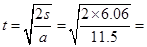
（1分）
s （1分）
点评：本题难度较大，对于多过程问题首先应选择好研究过程分析受力情况，利用牛顿第二定律结合运动学公式求解