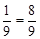问题
解答题
盒中有6只灯泡，其中2只次品，4只正品，有放回地从中任取两次，每次取一只，试求下列事件的概率：
(1)取到的2只都是次品；
(2)取到的2只中正品、次品各一只；
(3)取到的2只中至少有一只正品、
答案
(1)
(2)
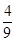(3) 
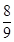
（1）从6只灯泡中有放回地任取两只，共有62种不同取法，则取到的2只都是次品1种，得到概率值。
（2）从6只灯泡中有放回地任取两只，共有62种不同取法．由于取到的2只中正品、次品各一只有两种可能，第一次取到正品，第二次取到次品；及第一次取到次品，第二次取到正品，根据相互独立事件同时发生的概率和互斥事件的概率，得到结果．
（3）取到的两只中至少有一只正品是取到的两只都是次品的对立事件，先做出两只都是次品的概率，再根据对立事件的概率公式，得到概率．
解：从6只灯泡中有放回地任取两只，共有62＝36种不同取法、
(1)取到的2只都是次品情况为22＝4种、因而所求概率为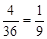
、(2)由于取到的2只中正品、次品各一只有两种可能：第一次取到正品，第二次取到次品；及第一次取到次品，第二次取到正品、因而所求概率为
P=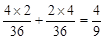
(3)由于“取到的两只中至少有一只正品”是事件“取到的两只都是次品”的对立事件、因而所求概率为P=1-