实系数一元二次方程x²+ax+2b-2=0有两个相异实根，f（x）=x²+ax+2b-2，图象开口向上，对称轴为x=-

a

2

，

∴

f(0)＞0 f(1)＜0 f(2)＞0

可得

2b-2＞0 1+a+2b-2＜0 4+2a+2b-2＞0

，

画出可行域：

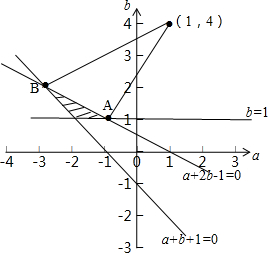
A点坐标为

b=1 a+2b-1=0

解得A（-1，1）；

B点坐标为

a+b+1=0 a+2b-1=0

解得B（-3，2）；

设目标函数z=

b-4

a-1

，表示可行域里面的点（a，b）与点p（1，4）的斜率的大小，

z_min=k_AP=

4-2

4

=

1

2

；

z_max=k_BP=

4-1

1+1

=

3

2

，

∴

1

2

≤z≤

3

2

，

∴

b-4

a-1

的取值范围是（

1

2

，

3

2

）；