问题
解答题
| 设f(x)=|lgx|,a,b为实数,且0<a<b. (1)求方程f(x)=1的解; (2)若a,b满足f(a)=f(b)=2f(
(3)在(2)的条件下,求证:由关系式f(b)=2f(
|
答案
(1)由f(x)=1得,lgx=±1,
所以x=10,或x=
.…(3分)1 10
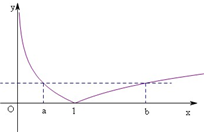
(2)证明:结合函数图象,由f(a)=f(b),
知a∈(0,1),b∈(1,+∞),…(4分)
从而-lga=lgb,从而ab=-1.…(5分)
又
=a+b 2
,…(6分)
+b1 b 2
令ϕ(b)=
+b(b∈(1,+∞).…(7分)1 b
任取1<b1<b2,
∵∅(b1)-∅(b2)=(b1-b2)(1-
)<0,1 b1b2
∴∅(b1)<∅(b2),
∴∅(b)在(1,+∞)上为增函数.
∴∅(b)>∅(1)=2.…(9分)
所以
>1.…(10分)a+b 2
(3)由b=(
)2,a+b 2
得4b=a2+b2+2ab,…(11分)
+b2+2-4b=0,1 b2
令g(b)=
+b2+2-4b,…(12分)1 b2
因为g(3)<0,g(4)>0,根据零点存在性定理知,…(13分)
函数g(b)在(3,4)内一定存在零点,
即方程
+b2+2-4b=0存在3<b<4的根.…(14分)1 b2
