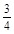（Ⅰ）（Ⅱ）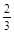

本题考查的知识点是几何概型与古典概型，根据已知条件计算全部基本事件的个数（几何量）和满足条件的基本事件的个数（几何量）是解答概率问题的关键．（1）（2）中没有结论或假设扣2分。

（1）由于a∈{0，1，2，3}，b∈{0，1，2}，则基本事件总数为3X4=12种，其中满足条件方程有实根，即△≥0，即a²+b²≥4共有8种，代入古典概型公式，即可得到答案．

（2）由于a∈[0，3]，b∈[0，2]，则基本事件对应的平面区域面积为3X2=6，其中满足条件方程有实根，即△≥0，即a²+b²≥4的平面区域面积为6-π，代入几何概型公式，即可得到答案．

解 设事件A为“方程x²+2ax+b²=0有实根”.

当a≥0,b≥0时，方程x²+2ax+b²=0有实根的充要条件为a≥b.

（1）基本事件共有12个：

（0，0），（0，1），（0，2），（1，0），（1，1），（1，2），（2，0），（2，1），（2，2），（3，0），（3，1），（3，2）.

其中第一个数表示a的取值，第二个数表示b的取值.

事件A中包含9个基本事件，事件A发生的概率为

P（A）==.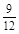

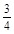（2）试验的全部结果所构成的区域为

{(a,b)|0≤a≤3,0≤b≤2}.

构成事件A的区域为

{(a,b)|0≤a≤3,0≤b≤2,a≥b}.

所以所求的概率为

P(A)=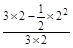=.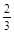