问题
解答题
某校为组建校篮球队，对报名同学进行定点投篮测试，规定每位同学最多投3次，每次在A或B处投篮，在A处投进一球得3分，在B处投进一球得2分，否则得0分，每次投篮结果相互独立，将得分逐次累加并用X表示，如果X的值不低于3分就认为通过测试，立即停止投篮，否则继续投篮，直到投完三次为止．投篮方案有以下两种：
方案1：先在A处投一球，以后都在B处投；
方案2：都在B处投篮．
已知甲同学在A处投篮的命中率为0.4，在B处投篮的命中率为0.6.
(1)甲同学若选择方案1，求X＝2时的概率；
(2)甲同学若选择方案2，求X的分布列和数学期望；
(3)甲同学选择哪种方案通过测试的可能性更大？请说明理由．
答案
（1）0.288（2）3.168（3）选择方案2通过测试的可能性更大
(1)“在A处投篮命中”记作事件A，不中记作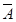
，“在B处投篮命中”记作事件B，不中记作
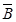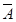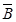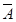
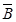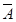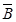，该同学选择方案1，测试结束后所得总分为2为事件(B)∪(B)，则其概率P1＝P(B)＋P(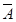 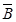B)＝(1－0.4)×0.6×(1－0.6)＋(1－0.4)×(1－0.6)×0.6＝0.288.
(2)该同学选择方案2，测试结束后，所得总分X所有可能取的值为0,2,4.
则P(X＝0)＝(1－0.6)×(1－0.6)×(1－0.6)＝0.064，
P(X＝2)＝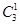
×0.6×0.42＝0.288，
P(X＝4)＝0.6×0.6＋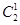
×0.62×0.4＝0.648，
∴X的分布列是
| X | 0 | 2 | 4 |
| P | 0.064 | 0.288 | 0.648 |
(3)设该同学选择方案1通过测试的概率为P2，P2＝P(A)＋P(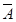BB)＝0.4＋(1－0.4)×0.6×0.6＝0.616，又选择方案2通过测试的概率P3＝0.648>0.616，所以该同学选择方案2通过测试的可能性更大．