问题
填空题
如图所示，在匀强电场中有A、B、C三点，在以它们为顶点的三角形中，∠A=30°，∠C=90°，电场方向与三角形所在平面平行．已知A、B、C三点的电势分别为（3-
）V、（3+3
） V和3V，则A、B连线中点处的电势为______V，该三角形外接圆上的最高电势为______ V．3
答案
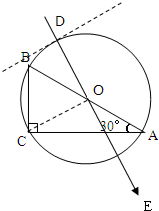
由U=Ed，U∝d（除等势面上），则A、B连线中点O的电势为A、B电势的平均值，即为3V．
连接OC线，即为一条等势线，作出过O的电场线OD和外接圆，逆着过O点的电场线，找出外接圆上离O点最远的D点，即为电势最高的点，根据几何知识得：
OD=OB，
由UDO=E•OD，UBO=E•OBcos30°
则得UDO=UBO•
=1 cos30°
V=2V，所以D点的电势为5V．即最高电势为5V．3 3 2
故答案为：3V，5V