问题
解答题
已知二次函数y=x2-6x+8.求:
(1)抛物线与x轴和y轴相交的交点坐标;
(2)抛物线的顶点坐标;
(3)画出此抛物线图象,利用图象回答下列问题:
①方程x2-6x+8=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
答案
(1)由题意,令y=0,得x2-6x+8=0,
解得x1=2,x2=4.
所以抛物线与x轴交点为(2,0)和(4,0),
令x=0,y=8.
所以抛物线与y轴交点为(0,8),
(2)抛物线解析式可化为:y=x2-6x+8=(x-3)2-1,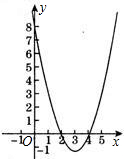
所以抛物线的顶点坐标为(3,-1),
(3)如图所示.
①由图象知,x2-6x+8=0的解为x1=2,x2=4.
②当x<2或x>4时,函数值大于0;
③当2<x<4时,函数值小于0;
