问题
计算题
如图所示,有一块木板静止在光滑且足够长的水平面上,木板的质量为M="4" kg,长度为L="1.4" m;木板的右端停放着一个小滑块,小滑块质量为m=1 kg,其尺寸远小于木板长度,它与木板间的动摩擦因数为μ=0.4,若滑块所受的最大静摩擦力是相同压力下滑动摩擦力的1.2倍,取g="10" m/s2,问:

(1)现用水平恒力F作用于木板上,为了能使木板能从滑块下抽出来,恒力F的大小范围是多少?
(2)若其它条件不变,水平恒力F=28 N,欲抽出木板,水平恒力至少要作用多长时间?
答案
(1)F≥24 N;(2)1 s
题目分析:(1)能使木板能从滑块下抽出来,滑块所受摩擦力必须大于最大静摩擦力。当滑块受最大静摩擦力时,根据牛顿第二定律有: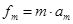
依题意有: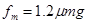
用整体法,对滑块和木板组成的系统,根据牛顿第二定律有;
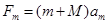
解得:Fm="24" N
可见恒力F的大小范围是F≥24 N。
恒力F作用下,根据牛顿第二定律有:
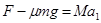
解得: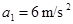
撤去F后,由牛顿第二定律可得:
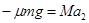
解得: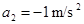
滑块: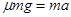
其加速度为: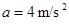
若F作用t1后撤去,滑块继续在木板上运动的时间为t2,根据匀变速直线运动的规律,木板运动的位移:
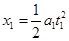
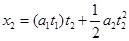
在整个时间内,滑块的位移为: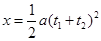
依题意有: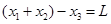
欲使时间最短,滑块和木板的末速度应该相等:
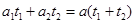
联立以上各式,解得:t1="1" s。
