班级联欢时，主持人拟出了如下一些节目：跳双人舞、独唱、朗诵等

问题解答题

班级联欢时，主持人拟出了如下一些节目：跳双人舞、独唱、朗诵等，指定3个男生和2个女生来参与，把5个人分别编号为1，2，3，4，5，其中1，2，3号是男生，4，5号是女生，将每个人的号分别写在5张相同的卡片上，并放入一个箱子中充分混合，每次从中随机地取出一张卡片，取出谁的编号谁就参与表演节目．

（I）为了选出2人来表演双人舞，连续抽取2张卡片，求取出的2人不全是男生的概率；

（Ⅱ）为了选出2人分别表演独唱和朗诵，抽取并观察第一张卡片后，又放回箱子中，充分混合后再从中抽取第二张卡片，求：独唱和朗诵由同一个人表演的概率．

答案

（I）利用树形图我们可以列出连续抽取2张卡片的所有可能结果（如下图所示）．

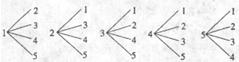
由上图可以看出，实验的所有可能结果数为20．

因为每次都随机抽取，因此这20种结果出现的可能性是相同的，属于古典概型．

用A₁表示事件“连续抽取2人，有1女生、1男生”，A₂表示事件“连续抽取2人都是女生”，

则A₁与A₂互斥，并且A₁∪A₂表示事件“连续抽取2张卡片，取出的2人不全是男生”，

由列出的所有可能结果可以看出，A₁的结果有12种，A₂的结果有2种，

由互斥事件的概率加法公式，可得P(A1∪A2)=P(A1)+P(A2)=

=0.7，

即连续抽取2张卡片，取出的2人不全是男生的概率为0.7．

（Ⅱ）有放回地连续抽取2张卡片，需注意同一张卡片可再次被取出，

并且它被取出的可能性和其他卡片相等，我们用一个有序实数对表示抽取的结果，

所有的可能结果可以用下表列出．

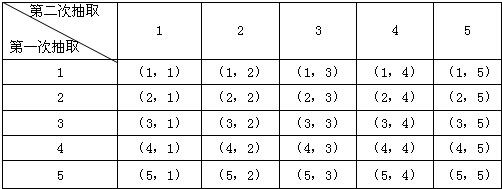
试验的所有可能结果数为25，并且这25种结果出现的可能性是相同的，试验属于古典型

用A表示事件“独唱和朗诵由同一个人表演”，由上表可以看出，A的结果共有5种，

因此独唱和朗诵由同一个人表演的概率P(A)=

=0.2．