问题
计算题
(23分)如图为一传送装置，倾角为α=53°的斜面AB与水平传送带在B处由一光滑小圆弧平滑衔接，可看作质点的货物从斜面上A点由静止下滑，经长度为S1的传送带后，最后抛入固定于水平地面上的圆弧形槽内。已知物体与斜面、传送带间的滑动摩擦因数均为μ=0.5，传送带两皮带轮的半径均为R1=0．4m，传送带上表面BC离地的高度h=1．2m。圆弧槽半径R2=1m，两边缘与圆心连线与竖直方向的夹角均为β=53°。当传送带静止时，将货物在斜面上离B点S2远处静止释放，货物脱离传送带后刚好沿圆弧槽左边缘D点的切线方向飞入槽内。当传送带顺时针转动时，无论传送带转多快，货物也不会从圆弧槽右边缘飞出，求：
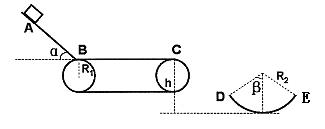
（1）传送带静止时，货物到达C点的速度大小和D点时的速度大小。
（2）求S1、S2的值应满足的关系。（sin53°= 0．8，cos53°= 0．6 ）
答案
（1）3m/s；5m/s；（2）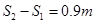
，
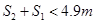
题目分析：（1）物体从C到D做平抛运动，水平方向速度不变
竖直方向下落的高度：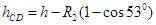
2分
因此到达D点时，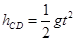
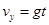1分
1分
得：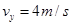
，
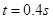
由于恰好沿切线飞入槽内，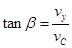
2分
代入数据：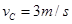
2分
可得
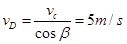2分
（2）若皮带不转，物体恰好落到D点
这样到达C点的速度为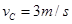
根据动能定理：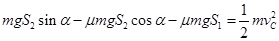
2分
代入数据整理得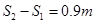： 2分
当皮带快速度转动时，恰好落到圆弧槽右边缘E点，
由于CD间的水平距离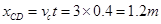
1分
从CE间水平距离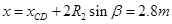
2分
因此平抛的初速度
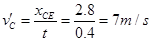2分
在这个运动过程中，在水平传送带上一直加速运动
根据动能定理：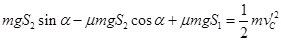
整理得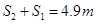
而若落到圆弧槽内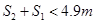 2分