问题
解答题
已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病,下面是两种化验方案:
方案甲:逐个化验,直到能确定患病动物为止。
方案乙:先任取3只,将它们的血液混在一起化验,若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验。
求依方案甲所需化验次数不少于依方案乙所需化验次数的概率。
答案
解:记A1、A2分别表示依方案甲需化验1次、2次,
B表示依方案乙需化验3次,
A表示依方案甲所需化验次数不少于依方案乙所需化验次数,
依题意知A2与B独立,且 ,
,
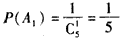 ,
,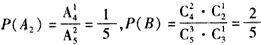 ,
,
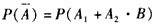
=P(A1)+P(A2·B)
=P(A1)+P(A2)·P(B)

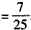 ,
,
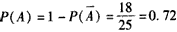 。
。
