问题
填空题
已知函数f(x)=|ax-1|-2a(a>0,且a≠1)有两个零点,则a的取值范围是______.
答案
设函数f(x)=|ax-1|-2a=0即|ax-1|=2a.
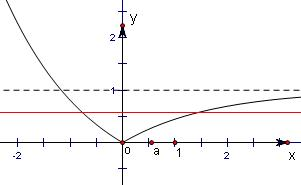
函数f(x)=|ax-1|-2a(a>0,且a≠1)有两个零点,即函数y=|ax-1|(a>0,且a≠1)与函数y=2a的图象有两个交点,
由图象可知当0<2a<1时两函数时,一定有两个交点.
所以实数a的取值范围是{a|0<a<
}.1 2
故答案为:(0,
).1 2