问题
解答题
一名射手在某次射击训练中，射中10环、9环、8环、7环的概率分别为0.21，0.23，0.25，0.28，计算这个射手在这次射击中：
（1）射中10环或7环的概率；
（2）射中的环数低于7环的概率。
答案
解：（1）设“射中10环”为事件A，“射中7环”为事件B，则“射中10环或7环”的事件为A∪B，
∴P（A∪B）=P（A）+P（B）=0.21+0.28=0.49，
∴射中10环或7环的概率为0.49；
（2）设“低于7环”为事件E，则事件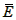
为“射中7环或8环或9环或10环”，
由于“射中7环”“射中8环”“射中9环”“射中10环”彼此互斥，
故P（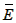
）=0.21+0.23+0.25+0.28=0.97，
从而P（E）=1-P（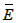
）=1-0.97=0.03，
∴射中的环数低于7环的概率为0.03。