问题
填空题
事实证明:总存在正实数a,b(a<b),使得ab=ba,请你写出所有符合条件的a的取值范围是______.
答案
∵ab=ba
∴lnab=lnba
又∵a,b是正实数
∴blna=alnb
∴
=lna a
,lnb b
设函数f(x)=
,则f′(x)=lnx x
,1-lnx x2
令f'(x)>0,得0<x<e;令f'(x)<0,得x>e
∴f(x)在(0,e)上单调递增,在(e,+∞)上单调递减
又当x→+∞时,f(x)→0且f(x)>0,
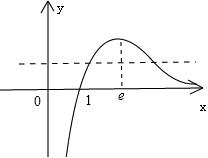
∴f(x)的图象如图所示:
又∵a<b,
∴1<a<e.
故答案为:(1,e).
