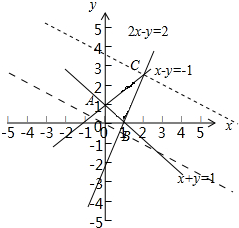∵x、y满足约束条件

x+y≥1 x-y≥-1 2x-y≤2

，目标函数z=ax+by（a＞0，b＞0），作出可行域：

由图可得，可行域为△ABC区域，目标函数z=ax+by（a＞0，b＞0）经过可行域内的点C时，取得最大值（最优解）．

由

x-y=-1 2x-y=2

解得x=3，y=4，即C（3，4），

∵目标函数z=ax+by（a＞0，b＞0）的最大值为7，

∴3a+4b=7（a＞0，b＞0），

∴

3

a

+

4

b

=

1

7

（3a+4b）•（

3

a

+

4

b

）

=

1

7

（9+

12b

a

+16+

12a

b

）≥

1

7

（25+2

12b a • 12a b

）=

1

7

×49=7（当且仅当a=b=1时取“=”）．

故选B．