解：令f(x)=2^x-x²，

∵f(-1)=2^-1-(-1)²=-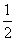＜0，f(0)=1＞0，

说明方程f(x)=0在区间(-1，0)内有一个零点；

取区间(-1，0)的中点x₁=-0.5，

用计算器可算得f(-0.5)≈0.46＞0，

因为f(-1)·f(-0.5)＜0，所以，x₀∈(-1，-0.5)；

再取(-1，-0.5)的中点x₂=-0.75，

用计算器可算得f(-0.75)≈-0.03＞0，

因为f(-1)·f(-0.75)＜0，所以x₀∈(-1，-0.75)；

同理，可得x₀∈(-0.875，-0.75)，x₀∈(-0.812 5，-0.75)，x₀∈(-0.781 25，-0.75)，

x₀∈(-0.781 25，-0.765 625)，x₀∈(-0.773 437 5，-0.765 625)，

由于|(-0.765 625)-(0.773 437 5)|＜0.01，

此时区间(-0.773 437 5，-0.765 625)的两个端点精确到0.01的近似值都是-0.77，

所以，方程2^x-x²=0精确到0.01的近似解约为-0.77.