问题
解答题
请先画一个直角三角形ABC,使∠C=90°,再画两锐角∠A,∠B的角平分线AO、BO交于点O.
(1)请计算∠AOB的度数;
(1)经过点O画直线DE∥AB交AC于点D,交BC于点E;其中有两个等腰三角形,找一个出来加以说明.
答案
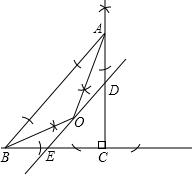
(1)Rt△ABC如图所示,
∵∠C=90°,
∴∠ABC+∠BAC=180°-90°=90°,
∵AO、BO分别是∠BAC、∠ABC的平分线,
∴∠OAB=
∠BAC,∠OBA=1 2
∠ABC,1 2
∴∠OAB+∠OBA=
(∠ABC+∠BAC)=1 2
×90°=45°,1 2
在△AOB中,∠AOB=180°-(∠OAB+∠OBA)=180°-45°=135°;
(2)等腰三角形有△BOE和△AOD.
以证明△AOD为例:
∵AO是∠BAC的平分线,
∴∠BAO=∠DAO,
∵DE∥AB,
∴∠BAO=∠AOD,
∴∠AOD=∠DAO,
∴AD=OD,
即△AOD是等腰三角形.