问题
计算题
（12分）一水平传送带以2.0m／s的速度顺时针传动，水平部分长为2.0m。，其右端与一倾角为θ=37°的光滑斜面平滑相连，斜面长为0.4m，一个可视为质点的物块无初速度地放在传送带最左端，已知物块与传送带间动摩擦因数μ=0.2，试问：
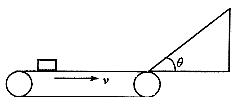
(1)物块能否到达斜面顶端?若能则说明理由，若不能则求出物块沿斜面上升的最大距离．
(2)物块从出发到4.5s末通过的路程．(sin37°=0.6， g取l0 m/s2)
答案
（1）s2<0.4m (2) s=5m
题目分析：（1）物块在传送带上先做匀加速直线运动
μmg=mal ① （1分）
②（1分）
所以在到达传送带右端前物块已匀速
物块以ν0速度滑上斜面
一mgsinθ=ma2 ③（1分）
物块速度为零时上升的距离
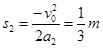④ （1分）
由于s2<0.4m，所以物块未到达斜面的最高点． （1分）
(2)（7分）物块从开始到第一次到达传送带右端所用时间
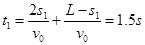⑥ （1分）
物块在斜面上往返一次时间
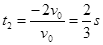⑦ （1分）
物块再次滑到传送带上速度仍为ν0，方向向左
一μmg =ma3 ⑧ （1分）
向左端发生的最大位移
⑨(2分)
物块向左的减速度和向右的加速过程中位移大小相等
4.5s末物块在斜面上速度恰好减为零
故物块通过的总路程
s=L+3s2+2s3 ⑩ (2分)
s=5m