问题
解答题
当m为何值时,方程x2-4|x|+5=m,(1)无解;(2)有两个实数解;(3)有三个实数解;(4)有四个实数解。
答案
解:设y1=x2-4|x|+5,y2=m,则该方程解的个数问题即可转化为
两个函数图象的交点个数问题来处理,
设y1=x2-4|x|+5,则y1=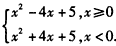 ,
,
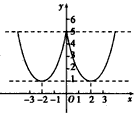
画出函数的图象,如右图所示,
再画出函数y2=m的图象,由图象可以看出:
(1)当m<1时,两个函数图象没有交点,故原方程无解;
(2)当m=1或m>5时,两个函数图象有两个交点,故原方程有两个解;
(3)当m=5时,两个函数图象有三个交点,故原方程有三个解;
(4)当1<m<5时,两个函数图象有四个交点,故原方程有四个解.