问题
计算题
(12分)如图所示，一质量为M的长木板静止在水平面上，有一质量为m的小滑块以一定的水平速度冲上木板，已知滑块和木板之间的动摩擦因数为
，最大静摩擦力等于滑动摩擦力，求
（1）若滑块在木板上滑动时，木板能保持静止不动，木板和地面之间的动摩擦因数须满足什么条件？
（2）若长木板的质量M=0.2kg，长木板与水平面间的动摩擦因数μ=0.1.滑块的质量也为0.2kg。滑块以v0=1.2m/s的速度滑上长板的左端，小滑块与长木板间的动摩擦因数μ0=0.4.滑块最终没有滑离长木板，求滑块在开始滑上长木板到最后静止下来的过程中，滑块滑行的距离是多少？（g=10m/s2）
答案
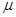
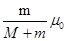0.24m
题目分析：（1）长木板受到滑块向前的摩擦力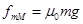
设长木板与地面之间的动摩擦因数为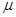
长木板受到地面的最大静摩擦力大小
由题意得：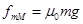
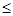
即：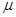
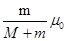
（2）对m：μ0mg=ma2 解得：a2=4m/s2
对M：μ0mg-μ(M+m)g=Ma1 解得：a1=2m/s2
设经历时间为t两者速度相同，则：v0-a2t=a1t
解得：t="0.2s"
两者共同速度为：v= a1t =0.4m/s
两者相对静止前，小滑块的位移：s1=v0t-a2t2/2=0.16m
达到共同速度后对滑块和木板：μ(M+m)g=（M+m）a3
滑行位移为：s2=v2/2a3 解得：s2=0.08m
小滑块的总位称为：s=s1+s2=0.24m