问题
解答题
判断方程3x-x2=0的负实数根的个数，并说明理由．
答案
解：设f(x)=3x-x2，
∵f(-1)=-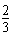
＜0，f(0)=1>0，
又∵函数f(x)的图象在[-1，0]上是连续不断的，
∴函数f(x)在(-1，0)内有零点，
又∵在(-∞，0)上，函数y=3x递增，y=x2递减，
∴f(x)在(-∞，0)上是单调递增的，
∴f(x)在(-1，0)内只有一个零点，
因此方程3x-x2=0只有一个负实数根．