问题
计算题
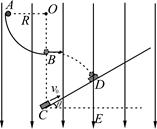
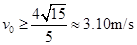（19分）如图所示，在竖直平面内固定一光滑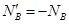
圆弧轨道AB，轨道半径为R＝0.4m，轨道最高点A与圆心O等高。有一倾角θ＝30°的斜面，斜面底端C点在圆弧轨道B点正下方、距B点H＝1.5m。圆弧轨道和斜面均处于场强E＝100N/C、竖直向下的匀强电场中。现将一个质量为m=0.02kg、带电量为
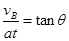的带电小球从A点静止释放，小球通过B点离开圆弧轨道沿水平方向飞出，当小球运动到斜面上D点时速度方向恰与斜面垂直，并刚好与一个以一定初速度从斜面底端上滑的物块相遇。若物块与斜面间动摩擦因数
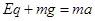，空气阻力不计，g取10m/s2，小球和物块都可视为质点。求：
（1）小球经过B点时对轨道的压力NB；
（2）B、D两点间电势差UBD；
（3）物块上滑初速度v0满足的条件。
答案
（1）
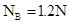，方向竖直向下（2）
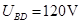（3）
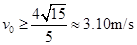
题目分析：（1）设小球到达B点的速度为vB，从A到B的过程只有重力和电场力做功，根据动能定理有：
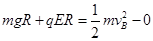
B点是圆周运动最低点，合力提供向心力即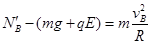
对轨道压力等于轨道对其弹力即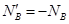
综上，解得：
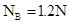，方向竖直向下。
（2）设小球由B点到D点的运动时间为t，受到竖直向下的重力和电场力，竖直方向为初速度0的匀加速直线运动，加速度为a，水平方向没力为匀速直线遇到你。下落高度为h的过程
根据速度合成有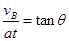
竖直方向牛顿第二定律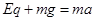
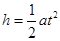
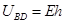
联立解得
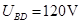
（3）作出小球与物块的运动示意如图所示，设C、D间的距离为x，由几何关系有：
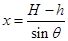
设物块上滑加速度为a′，由牛顿运动定律有：
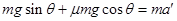
根据题意，要物块与小球相遇，有：
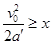
联解得：