问题
解答题
在某次趣味运动会中,甲、乙、丙三名选手进行单循环赛(即每两人比赛一场),共赛三场,每场比赛胜者得1分,输者得0分,没有平局;在每一场比赛中,甲胜乙的概率为
(Ⅰ)求甲获得小组第一且丙获得小组第二的概率; (Ⅱ)求三人得分相同的概率; (Ⅲ)设在该小组比赛中甲得分数为ξ,求Eξ. |
答案
(Ⅰ)设甲获小组第一且丙获小组第二为事件A,
所有场次为(甲、乙)、(甲、丙)、(乙、丙)
则甲获小组第一且丙获小组第二为甲胜两场,丙胜一场
所以P(A)=
×1 3
×1 4
=2 3 1 18
(Ⅱ)设三场比赛结束后,三人得分相同为事件B,
即每人胜一场输两场,有以下两种情形:
甲胜乙,乙胜丙,丙胜甲,概率为P1=
×1 3
×1 3
=3 4
,1 12
甲胜丙,丙胜乙,乙胜甲,概率为P2=
×1 4
×2 3
=2 3
,1 9
三人得分相同的概率为P(B)=P1+P2=
+1 12
=1 9
.7 36
(Ⅲ)ξ可能的取值为0、1、2,
P(ξ=0)=
×2 3
=3 4
,P(ξ=1)=1 2
×1 3
+3 4
×1 4
=2 3
,5 12
P(ξ=2)=
×1 3
=1 4
,1 12
所以ξ的分布列为:
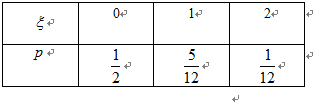
Eξ=0×
+1×1 2
+2×5 12
=1 12
.7 12
