问题
填空题
若实数x,y满足x2+y2+xy=1,则x+y的最大值是 .
答案
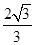
∵xy≤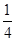 (x+y)2,
(x+y)2,
∴1=x2+y2+xy
=(x+y)2-xy
≥(x+y)2-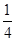 (x+y)2
(x+y)2
=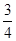 (x+y)2,
(x+y)2,
∴(x+y)2≤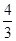 ,
,
∴-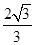 ≤x+y≤
≤x+y≤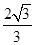 ,
,
当x=y=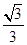 时,x+y取得最大值
时,x+y取得最大值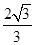 .
.
若实数x,y满足x2+y2+xy=1,则x+y的最大值是 .
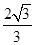
∵xy≤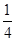 (x+y)2,
(x+y)2,
∴1=x2+y2+xy
=(x+y)2-xy
≥(x+y)2-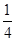 (x+y)2
(x+y)2
=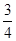 (x+y)2,
(x+y)2,
∴(x+y)2≤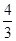 ,
,
∴-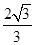 ≤x+y≤
≤x+y≤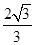 ,
,
当x=y=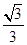 时,x+y取得最大值
时,x+y取得最大值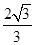 .
.