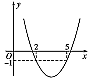问题
证明题
判定方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于2。
答案
证明:设函数f(x)=(x-2)(x-5)-1,
有f(5)=(5-2)(5-5)-1=-1, f(2)=(2-2)(2-5)-1=-1,
又因为f(x)的图象是开口向上的抛物线(如右图所示),
所以抛物线与横轴在(5,+∞)内有一个交点,在(-∞,2)内也有一个交点,
所以方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于2。