问题
选择题
若x2＋xy＋y2＝1且x、y∈R，则n＝x2＋y2的取值范围是( )
A．0＜n≤1
B．2≤n≤3
C．n≥2
D．≤n≤2
答案
答案：D
分析：先根据x2+xy+y2=1得到xy=1-（x2+y2），再由基本不等式和绝对值不等式得到-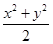 
≤-|xy|≤xy≤|xy|≤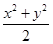，再将xy=1-（x2+y2）代入即可得到答案．
解：x2+xy+y2=1，
∴xy=1-（x2+y2），
又-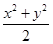≤-|xy|≤xy≤|xy|≤，
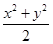知-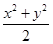≤1-（x2+y2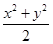）≤，得出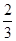
≤x2+y2≤2．
故选D
