解：（1）f′（x）=a^xlna+2x﹣lna=2x+（a^x﹣1）lna  

由于a＞1，

故当x∈（0，+∞）时，lna＞0，ax﹣1＞0，所以f′（x）＞0，

故函数f（x）在（0，+∞）上单调递增  

（2）当a＞0，a≠1时，

因为f′（0）=0，且f′（x）在R上单调递增，

故f′（x）=0有唯一解x=0

所以x，f′（x），f（x）的变化情况如下表所示：

又函数y=|f（x）﹣t|﹣1有三个零点，

所以方程f（x）=t±1有三个根，

而t+1＞t﹣1，

所以t﹣1=（f（x））_min=f（0）=1，

解得t=2；

（3）因为存在x₁，x₂∈[﹣1，1]，使得|f（x₁）﹣f（x₂）|≥e﹣1，

所以当x∈[﹣1，1]时，

|（f（x））_max﹣（f（x））_min|

=（f（x））_max﹣（f（x））_min

≥e﹣1，

由（Ⅱ）知，f（x）在[﹣1，0]上递减，在[0，1]上递增，

所以当x∈[﹣1，1]时，（f（x））_min=f（0）=1，

（f（x））_max=max{f（﹣1），f（1）}，

而，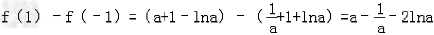

记，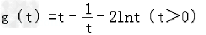

因为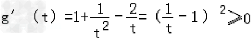（当t=1时取等号），

所以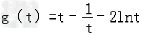在t∈（0，+∞）上单调递增，

而g（1）=0，

所以当t＞1时，g（t）＞0；

当0＜t＜1时，g（t）＜0，也就是当a＞1时，f（1）＞f（﹣1）；

当0＜a＜1时，f（1）＜f（﹣1）

①当a＞1时，由f（1）﹣f（0）≥e﹣1a﹣lna≥e﹣1a≥e，

②当0＜a＜1时，由，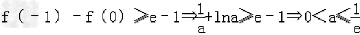

综上知，所求a的取值范围为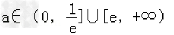．