问题
问答题
（本题12分）要求摩托车由静止开始在尽量短的时间内走完一段直道，然后驶入一段半圆形的弯道但在弯道上行驶时车速不能太快，以免因离心作用而偏出车道。求摩托车在直道上行驶所用的最短时间。有关数据见表格。
某同学是这样解的：要使摩托车所用时间最短，应先由静止加速到最大速度 v1＝40 m/s，然后再减速到v2＝20 m/s，
t1 =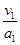 
= …； t2 = 
= …； t = t1 + t2
你认为这位同学的解法是否合理？若合理，请完成计算；若不合理，请说明理由，并用你自己的方法算出正确结果。
答案
不合理；理由见解析；11s
题目分析：这位同学的解法不合理．因为按这位同学的解法可得 ：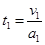
及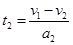
代入数据解得：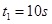
，
．
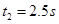所以加速距离
减速距离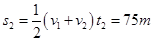
总位移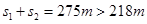
这说明当达到最大速度之后再减速的总的位移的大小要大于直道的长度，即摩托车不能达到最大的速度，否则达到弯道时就要偏出车道；最短的时间应该是摩托车以最大的加速度加速之后接着以最大的加速度减速运动，达到弯道时的速度恰好为弯道最大速度v2，故不合理．
由上可知摩托车不能达到最大速度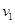
，设满足条件的最大速度为
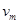，则：
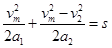解得：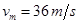
又加速的时间为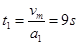
减速的时间为
因此所用的最短时间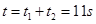
．