问题
解答题
射击运动员在双项飞碟比赛中,每轮比赛连续发射两枪,击中两个飞靶得2分,击中一个飞靶得1分,不击中飞靶得0分,某射击运动员在每轮比赛连续发射两枪时,第一枪命中率为
(Ⅰ)求该运动员得4分的概率为多少? (Ⅱ)若该运动员所得分数为,求的分布列及数学期望. |
答案
(I)设运动员得4分的事件为A,
得4分时,即两轮都击中两个飞靶,
则P(A)=
,4 81
(Ⅱ)设运动员得i分的事件为,
ξ的可能取值为0,1,2,3,4;
P(ξ=0)=P(ξ=4)=
,4 81
P(ξ=1)=P(ξ=3)=
,20 81
P(ξ=2)=
,33 81
ξ的分布列为:
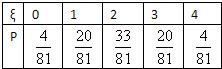
数学期望Eξ=0×
+1×4 81
+2×20 81
+3×33 81
+4×20 81
=2.4 81
