解：(Ⅰ)，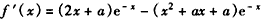

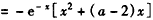令f′(x)=0，解得：x=0或x=2-a，

①当a=2时，f′(x)≤0，此时无极值；

②当0＜2-a，即a＜2时，f′(x)和f(x)的变化如下表1，

此时应有f(0)=0，所以，a=0＜2；

③当0＞2-a，即a＞2时，f′(x)和f(x)的变化如下表2，

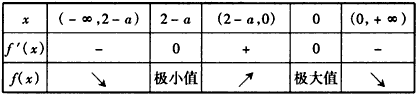
此时应有f(2-a)=0，即，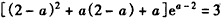

所以必有；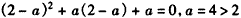

综上所述，当a=0或a=4时，f(x)的极小值为0。

(Ⅱ)若a＜2，则由表1知，应有f(2-a)=3，

即，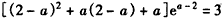

∴，

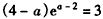设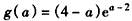，则，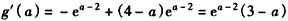

由a＜2，故g′(x)＞0，

于是当a＜2时，g(a)＜g(2)=2＜3，即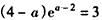不可能成立；

若a＞2，则由表2知，应有f(0)=3，即a=3；

综上所述，当且仅当a=3时极大值为3。

(Ⅲ) ∵，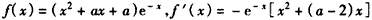

∴方程可以化为，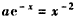

进而化为，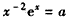

构造函数，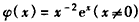

求导可得，，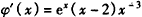

由ψ′(x)＞0得x＜0或x＞2，由ψ′(x)＜0得0＜x＜2，

从而ψ(x)在区间(-∞，0)和(2，+∞)上单调递增，在区间（0，2）上单调递减，

当x=2时，函数ψ(x)取得极小值。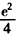

并且结合函数图象可知：当|x|无限趋近于0时，ψ(x)＞0并且取值无限增大，其图象向上无限接近y轴，但永远也达不到y轴（此时y轴足渐近线）；

当x＜0并无限减小时，ψ(x)＞0并且取值也无限减小，其图象在 x轴上方并向左无限接近x轴，但永远也达不到x轴（此时x轴是渐近线）；

当x＞2并无限增大时，ψ(x)＞0并且取值也无增大，其图象在第一象限内向右上方无限延伸（如图所示）

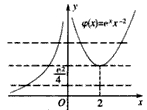
因此，当a≤0时，原方程无实根；

当0＜a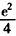＜时，原方程只有一个实数根；

当a=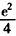时，原方程有两个不等的实数根；

当a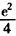＞时，原方程有三个不等的实数根。