某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆900元的保险金、对在一年内发生此种事故的每辆汽车,单位获9000元的赔偿(假设每辆车最多只赔偿一次).设这三辆车在一年内发生此种事故的概率分别为
(1)获赔的概率; (2)获赔金额ξ的分别列与期望. |
(1)设Ak表示第k辆车在一年内发生此种事故,k=1,2,3,
由题意知A1,A2,A3独立,且P(A1)=
,P(A2)=1 9
,P(A3)=1 10 1 11
∵该单位一年内获赔的对立事件是A1,A2,A3都不发生,
∴该单位一年内获赔的概率为1-P(. A1 . A2
)=1-P(. A3
)P(. A1
)P(. A2
)=1-. A3
×8 9
×9 10
=10 11
.3 11
(Ⅱ)ξ的所有可能值为0,9000,18000,27000
P(ξ=0)=P(. A1 . A2
)=P(. A3
)P(. A1
)P(. A2
)=. A3
×8 9
×9 10
=10 11
,8 11
P(ξ=9000)=P(A1. A2
)+P(. A3
A2. A1
)+P(. A3 . A1
A3). A2
=P(A1)P(
)P(. A2
)+P(. A3
)P(A2)P(. A1
)+P(. A3
)P(. A1
)P(A3). A2
=
×1 9
×9 10
+10 11
×8 9
×1 10
+10 11
×8 9
×9 10
=1 11
=242 990
,11 45
P(ξ=18000)=P(A1A2
)+P(A1. A3
A3)+P(. A2
A2A3). A1
=P(A1)P(A2)P(
)+P(A1)P(. A3
)P(A3)+P(. A2
)P(A2)P(A3). A1
=
×1 9
×1 10
+10 11
×1 9
×9 10
+1 11
×8 9
×1 10
=1 11
=27 990
,3 110
P(ξ=27000)=P(A1A2A3)=P(A1)P(A2)P(A3)
=
×1 9
×1 10
=1 11
,1 990
综上知,ξ的分布列为
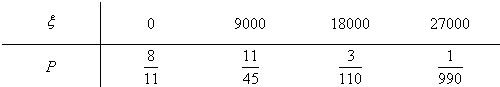
设ξk表示第k辆车一年内的获赔金额,k=1,2,3,则ξ1有分布列
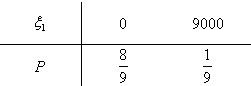
∴Eξ1=9000×
=10001 9
同理得Eξ2=9000×
=900,Eξ3=9000×1 10
≈818.181 11
综上有Eξ=Eξ1+Eξ2+Eξ3≈1000+900+818.18=2718.18(元)
