问题
解答题
设f（x）=ax2+（b﹣8）x﹣a﹣ab，不等式f（x）＞0的解集是（﹣3，2）．
（1）求f（x）；
（2）当函数f（x）的定义域是[0，1]时，求函数f（x）的值域．
答案
解：（1）∵f（x）＞0的解集是（﹣3，2），
∴﹣3，2是方程ax2+（b﹣8）x﹣a﹣ab=0的两个根，
∴﹣3+2=﹣1=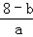
，即b﹣8=a①
﹣3×2=﹣6=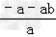
，即1+b=6②
解得a=﹣3，b=5
∴f（x）=﹣3x2﹣3x+18
（2）∵函数f（x）=﹣3x2﹣3x+18的图象是以x=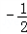
为对称轴，开口方向朝下的抛物线
故函数f（x）=﹣3x2﹣3x+18在区间[0，1]上单调递减
∴当x=0时，y有最大值18，当x=1时，y有最小值12，
∴当x∈[0，1]时函数f（x）的值域[12，18]