问题
填空题
直线y=1与曲线y=x2-|x|+a有两个交点，则a的取值范围是______．
答案
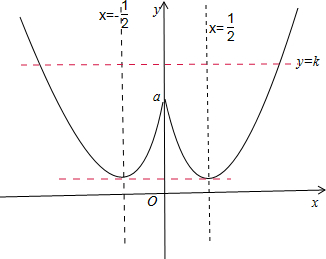
∵曲线y=x2-|x|+a=
，作出函数图象：(x-
)2+a-1 2
，当x≥0时1 4 (x+
)2+a-1 2
，当x＜0时1 4
由图象可知：若使直线y=1与曲线y=x2-|x|+a有两个交点，
则满足a＜1或a-
=1，1 4
故答案为a＜1或a=
．5 4
搜题请搜索小程序“爱下问搜题”
