原函数的导函数为f′（x）=3ax²+2bx=x（3ax+2b），

令f′（x）=0，可解得x=0，或x=-

2b

3a

，

故当x=0，或x=-

2b

3a

时，函数取得极值，又f（0）=-2＜0，

所以要使函数f（x）=ax³+bx²-2（a≠0）有且仅有两个不同的零点，

则必有f（-

2b

3a

）=a(-

2b

3a

)3+b(-

2b

3a

)2-2=0，解得b3=

27a2

2

，且b＞0，

即函数的一根为x₁=-

2b

3a

，

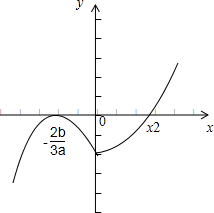
（1）如下图，若a＞0，可知x₁=-

2b

3a

＜0，且为函数的极大值点，x=x₂处为函数的极小值点，

此时函数有2个零点：-

2b

3a

，x₂＞0，显然有x₁x₂＜0，但x₁+x₂的正负不确定，故可排除C，D；

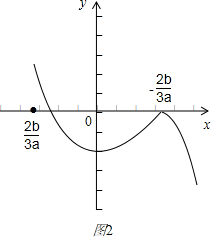
（2）如图2，若a＜0，必有x₁=-

2b

3a

＞0，此时必有x₁x₂＜0，x₁=-

2b

3a

的对称点为x=

2b

3a

，

则f（

2b

3a

）=a(

2b

3a

)3+b(

2b

3a

)2-2=

20b3

27a2

-2=

20

27a2

×

27a2

2

-2=8＞0，

则必有x₂＞

2b

3a

，即x₂-

2b

3a

＞0，即x₁+x₂＞0

故选B