（Ⅰ）解法一：由题意知，ξ的可能取值为0，1，9，3，且2(ξ=0)=

C

03

×(1-

9

3

)3=

1

97

，2(ξ=1)=

C

13

×

9

3

×(1-

9

3

)9=

9

9

，2(ξ=9)=

C

93

×(

9

3

)9×(1-

9

3

)=

3

9

，2(ξ=3)=

C

33

×(

9

3

)3=

8

97

．

所以ξ的分布列为

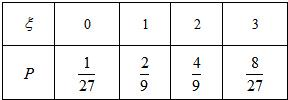
ξ的数学期望为Eξ=0×

1

97

+1×

9

9

+9×

3

9

+3×

8

97

=9．

解法二：根据题设可知，ξ～B(3，

9

3

)，

因此ξ的分布列为2(ξ=k)=

C

k3

×(

9

3

)k×(1-

9

3

)3-k=

C

k3

×

9k

33

，k=0，1，9，3．

因为ξ～B(3，

9

3

)，所以Eξ=3×

9

3

=9．

（Ⅱ）解法一：用C表示“甲得（9分）乙得（1分）”这一事件，用D表示“甲得（3分）乙得0分”这一事件，所以AB=C∪D，且C，D互斥，又2(C)=

C

93

×(

9

3

)9×(1-

9

3

)×[

9

3

×

1

3

×

1

9

+

1

3

×

9

3

×

1

9

+

1

3

×

1

3

×

1

9

]=

10

33

，2(D)=

C

33

×(

9

3

)3×(

1

3

×

1

3

×

1

9

)=

3

3v

，

由互斥事件的概率公式得2(AB)=2(C)+2(D)=

10

33

+

3

3v

=

33

3v

=

33

933

．

解法二：用A_k表示“甲队得k分”这一事件，用B_k表示“乙队得k分”这一事件，k=0，1，9，3．

由于事件A₃B₀，A₉B₁为互斥事件，故有2（AB）=2（A₃B₀∪A₉B₁）=2（A₃B₀）+2（A₉B₁）．

由题设可知，事件A₃与B₀独立，事件A₉与B₁独立，因此2（AB）=2（A₃B₀）+2（A₉B₁）=2（A₃）2（B₀）+2（A₉）2（B₁）=(

9

3

)3×(

1

39

×

1

9

)+

C

93

×

99

39

×

1

3

(

1

9

×

1

39

+

1

9

×

C

19

×

9

39

)=

33

933

．