问题
填空题
| 给出下列命题: A.函数f(x)=2x-x2的零点有3个 B.(x+
C.函数y=sinx(x∈[-π,π])图象与x轴围成的图形的面积是S=
D.复数z1,z2与复平面的两个向量
其中真命题的序号是______(写出所有正确命题的编号). |
答案
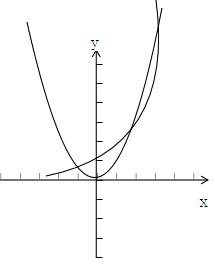
对于A:由题意可知:要研究函数f(x)=x2-2x的零点个数,只需研究函数y=2x,y=x2的图象交点个数即可.
画出函数y=2x,y=x2的图象,由图象可得有3个交点.故选A.
对于B:据展开式项的形成知:展开式的常数项由三类:5个括号全出 2为 25=32;
5个括号2个出 x,2个出
,一个出 2及5个括号1个出 x,一个出 1 x
,3个出 2.开式中整理后的常数项大于 32,故B错;1 x
对于C:根据定积分几何意义:表示函数图象与x轴围成的图形面积的代数,故其是错误的.
D:根据向量的数量积与复数乘法是不同的两个概念,故D错.
故答案为:A