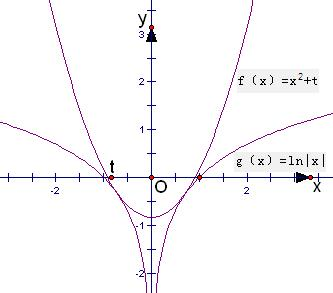
由于函数f（x）和函数g（x）都是偶函数，图象关于y轴对称，故当这两个函数在（0，+∞）上有2个交点时，函数f（x）=x²+t的图象与函数g（x）=ln|x|的图象有四个交点．

当x＞0时，令 h（x）=f（x）-g（x）=x²+t-lnx，则 h′（x）=2x-

1

x

．

令h′（x）=0可得x=

2

2

，故这两个函数的图象在（0，+∞）上相切时切点的横坐标为x=

2

2

．

当x=

2

2

时，f（x）=

1

2

+t，g（x）=ln

1

2

=-ln2，

函数f（x）=x²+t的图象与函数g（x）=ln|x|的图象有四个交点，应有

1

2

+t＜-ln2，

由此可得 t＜-

1

2

-ln2，故实数m的取值范围为 （-∞，-

1

2

-ln2），

故答案为 （-∞，-

1

2

-ln2）．