搜题请搜索小程序“爱下问搜题”
问题 选择题
若直线y=x+m与曲线y=3-
x(4-x)
有公共点，则m所的取值范围是（　　）
A．[1-2
2
，1+2
2
]		B．[1-2
2
，3]		C．[1-
2
，3]		D．[-1，1+2
2
]
答案

由x（4-x）≥0，得0≤x≤4．由y=3-

x(4-x)
得（y-3）2=x（4-x）=-x2+4x，且y≤3．

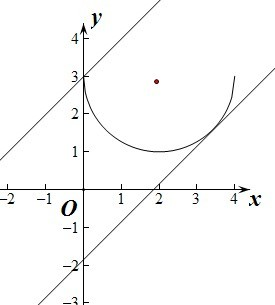
即（x-2）2+（y-3）2=4，因为0≤x≤4，所以曲线为圆心为（2，3），半径为2的下半圆．

圆心到直线距离d=

|2-3+m|
12+12
=
|m-1|
2
，由
|m-1|
2
≤2，解得1-2
2
≤m≤1+2
2
．

因为圆是下半圆，所以当直线y=x+m经过点（0，3）时，m取到最大值3，所以1-2

2
≤m≤3．即m所的取值范围是[1-2
2
，3]．

故选B．

材料分析题

材料一：由国家有关部委和深圳市人民政府联合主办的“高交会”，已举办了十一届。它为企业创新发展营造了良好的环境，搭建了展示的平台。QQ、U盘、数字电视、蓝牙等高科技产品从这里起步，众多人们熟知的高科技企业在这里起航。“高交会”已成为创新力的“催生剂”、产学研的“立交桥”、产业链的“联接器”、全球化的“桥头堡”，在提高我国自主创新能力的进程中发挥了巨大作用。

材料二：创立于1998年11月的腾讯公司，曾经举步维艰。马化腾带领他的团队四处寻求出路。“高交会”及时为企业发展解困，为“小企鹅”插上腾飞的翅膀。同时，公司紧盯市场，通过革新技术，让QQ登陆手机等无线即时通讯设备，拓展QQ的生存空间，企业不断发展壮大。2009年，公司市值突破400亿美元，成为市值全球排名第三的互联网公司。腾讯公司用互联网等先进技术不断提升人们的生活品质，形成了政府、企业、消费者多赢的局面。

材料三：长期以来，国外动漫一直掌控着我国市场的主要份额，国内动漫产业在夹缝中艰难生存。由广东原创动力文化传播有限公司出品的《喜羊羊与灰太狼》打破了这种格局。该动漫片自播出以来，已生成了4亿元左右的经济效益；“喜、羊羊”身后的产业链也是枝繁叶茂，衍生品的种类从图书、玩具、服装扩展到了文具、日化，乃至食品、手机、QQ等，成为人们喜闻乐见的文化产品。“喜羊羊”令国内动漫产业喜洋洋。

（1）根据材料一、二，从《政治生活》角度谈谈政府为企业创新发展提供服务的依据。

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

（2）联系材料二、三，从《文化生活》角度说明我国文化产业的发展对社会的影响。

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

（3）结合材料二，运用唯物辩证法的发展观分析腾讯公司是如何进行创新发展的。

_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
查看答案
单项选择题

合伙企业数量较多，但是规模同样较小，尤为（）形式居多。

A.小型企业

B.家族企业

C.中型企业

D.集体企业
查看答案