已知函数f(x)=(x2-3x+3)ex.
(Ⅰ)如果f(x)定义在区间[-2,t](t>-2)上,那么
①当t>1时,求函数y=f(x)的单调区间;
②设m=f(-2),n=f(t).试证明:m<n;
(Ⅱ)设g(x)=f(x)+(x-2)ex,当x>1时,试判断方程g(x)=x根的个数.
(I)f′(x)=(2x-3)ex+(x2-3x+3)ex=x(x-1)ex.
①当t>1时,
当x∈(-2,0)时,f′(x)>0,函数f(x)单调递增;
当x∈(0,1)时,f′(x)<0,函数f(x)单调递减;
当x∈(1,t)时,f′(x)>0,f(x)单调递增.
综上可知:当x∈(-2,0),(1,t)时,函数f(x)单调递增;当x∈(0,1)时,函数f(x)单调递减.
②设h(t)=n-m=(t2-3t+3)et-13e-2,h′(t)=t(t-1)et(t>2),列表如下:
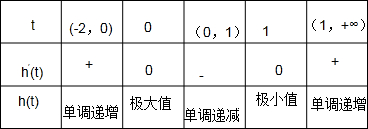
由表格可知h(t)的极小值为h(1)=e-
=13 e2
>0,而h(-2)>0,e3-13 e2
∴当t>-2时,h(t)>h(-2),即n>m.
(II)g(x)=(x2-3x+3)ex+(x-2)ex=(x-1)2ex,
问题转化为:判定方程(x-1)2ex=x当x>1时,根的个数.
设u(x)=(x-1)2ex-x(x>1),则u′(x)=(x2-1)ex-1,
设v(x)=(x2-1)ex-1(x>1),则v′(x)=(x2+2x-1)ex,
当x>1时,v′(x)>0,v(x)在(1,+∞)上单调递增,而v(1)=-1<0,v(2)=3e2-1>0,
因此在(1,2)上存在唯一x0,使得v(x0)=0,即存在唯一x0∈(1,2)使得u′(x0)=0,
列表如下:
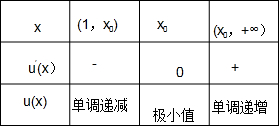
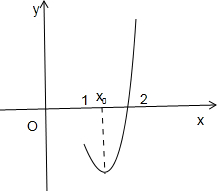
可知:u(x)min=u(x0)<u(1)=-1<0,由u(2)=e2-2>0,y=u(x)的图象如图所示,因此y=u(x)在(1,+∞)只有一个零点,即g(x)=x(x>1)只有一个零点.
