已知a＞0，函数f（x）=lnx-ax2，x＞0．（f（x）的图象连续不断）（Ⅰ

问题解答题

已知a＞0，函数f（x）=lnx-ax²，x＞0．（f（x）的图象连续不断）
（Ⅰ）求f（x）的单调区间；
（Ⅱ）当a=

时，证明：存在x₀∈（2，+∞），使f(x0)=f(

)；
（Ⅲ）若存在均属于区间[1，3]的α，β，且β-α≥1，使f（α）=f（β），证明

ln3-ln2

≤a≤

ln2

．

答案

（I）f′(x)=

-2ax=

1-2ax2

，x∈(0，+∞)，

令f′(x)=0，解得x=

．

当x变化时，f'（x），f（x）的变化情况如下表：

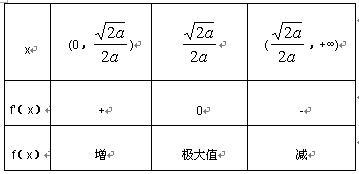
所以，f（x）的单调递增区间是(0，

)，f(x)的单调递减区间是(

，+∞)．

（II）证明：当a=

时，f(x)=lnx-

x2．

由（I）知f（x）在（0，2）内单调递增，

在（2，+∞）内单调递减．

令g(x)=f(x)-f(

)．

由于f（x）在（0，2）内单调递增，

故f(2)＞f(

)，即g(2)＞0．

取x′=

e＞2，则g(x′)=

41-9e2

＜0．

所以存在x₀∈（2，x'），使g（x₀）=0，

即存在x0∈(2，+∞)，使f(x0)=f(

)．

（说明：x'的取法不唯一，只要满足x'＞2，且g（x'）＜0即可）

（III）证明：由f（α）=f（β）及（I）的结论知α＜

＜β，

从而f（x）在[α，β]上的最小值为f（a）．

又由β-α≥1，α，β∈[1，3]，知1≤α≤2≤β≤3．

故

f(2)≥f(α)≥f(1)

f(2)≥f(β)≥f(3).

即

ln2-4a≥-a

ln2-4a≥ln3-9a.

从而

ln3-ln2

≤a≤

ln2

．