(19分)如图所示,竖直固定的光滑绝缘的直圆筒底部放置一场源A,其电荷量Q = +4×10-3 C,场源电荷A形成的电场中各点的电势表达式为 ,其中k为静电力恒量,r为空间某点到A的距离.有一个质量为
,其中k为静电力恒量,r为空间某点到A的距离.有一个质量为 的带正电小球B,B球与A球间的距离为a =" 0.4" m,此时小球B处于平衡状态,且小球B在场源A形成的电场中具有的电势能表达式为
的带正电小球B,B球与A球间的距离为a =" 0.4" m,此时小球B处于平衡状态,且小球B在场源A形成的电场中具有的电势能表达式为 ,其中r为q与Q之间的距离.有一质量也为m的不带电绝缘小球C从距离B的上方H =" 0.8" m处自由下落,落在小球B上立刻与小球B粘在一起向下运动,它们到达最低点后又向上运动,它们向上运动到达的最高点P.(取
,其中r为q与Q之间的距离.有一质量也为m的不带电绝缘小球C从距离B的上方H =" 0.8" m处自由下落,落在小球B上立刻与小球B粘在一起向下运动,它们到达最低点后又向上运动,它们向上运动到达的最高点P.(取 ,
, ),求:
),求:

(1)小球C与小球B碰撞后的速度为多少?
(2)小球B的带电量q为多少?
(3)P点与小球A之间的距离为多大?
(4)当小球B和C一起向下运动与场源A距离多远时,其速度最大?速度的最大值为多少?
(1)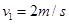 (2)
(2)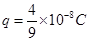 (3)
(3)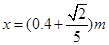 (4)
(4)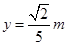 ,
,
题目分析:(1)小球C自由下落H距离的速度 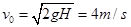 (2分)
(2分)
小球C与小球B发生碰撞,由动量守恒定律得: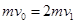 ,所以
,所以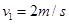 (2分)
(2分)
(2)小球B在碰撞前处于平衡状态,对B球进行受力分析知:
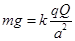 , 代入数据得:
, 代入数据得: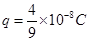 (2分)
(2分)
(3)C和B向下运动到最低点后又向上运动到P点,运动过程中系统能量守恒,设P与A之间的距离为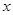 ,由能量守恒定律得:
,由能量守恒定律得:
 (4分)
(4分)
代入数据得: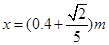 (或
(或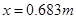 ) (2分)
) (2分)
(4)当C和B向下运动的速度最大时,与A之间的距离为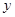 ,对C和B整体进行受力分析有:
,对C和B整体进行受力分析有:
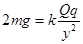 ,代入数据有:
,代入数据有: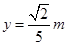 (或
(或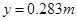 ) (3分)
) (3分)
由能量守恒定律得: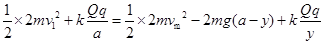 (3分)
(3分)
代入数据得: (或
(或 ) (1分)
) (1分)
